This browser is no longer supported.
Upgrade to Microsoft Edge to take advantage of the latest features, security updates, and technical support.
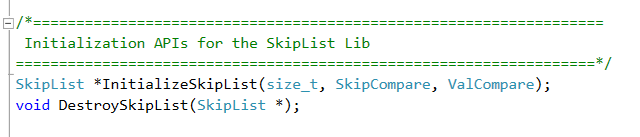
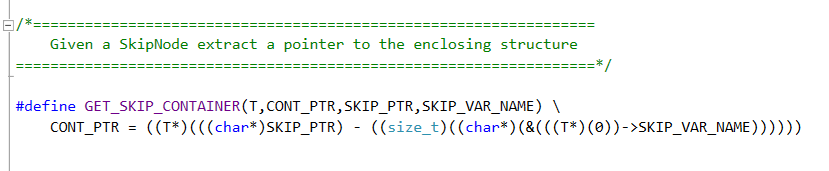 This Macro is not simple to understand so I suggest examining it carefully to see what it does. However, I will mention that it uses the relative location of the SkipNode variable inside the enclosing structure to get the address of the enclosing structure. This is a worthwhile trick to master by itself.
This Macro is not simple to understand so I suggest examining it carefully to see what it does. However, I will mention that it uses the relative location of the SkipNode variable inside the enclosing structure to get the address of the enclosing structure. This is a worthwhile trick to master by itself.