KMP Algorithm and its less obvious applications
Today I'd like to talk about an algorithm that I believe should be in any Software Engineer's toolkit. That is, the KMP algorithm named after its three inventors: Knuth-Morris-Pratt. The algorithm was designed to solve efficiently a very common problem. That is the problem of finding whether or not one string is a substring of a different string. While I will definitely dwell on this original problem, I will also show an example that is less obvious of how this algorithm can be used to solve string problems efficiently.
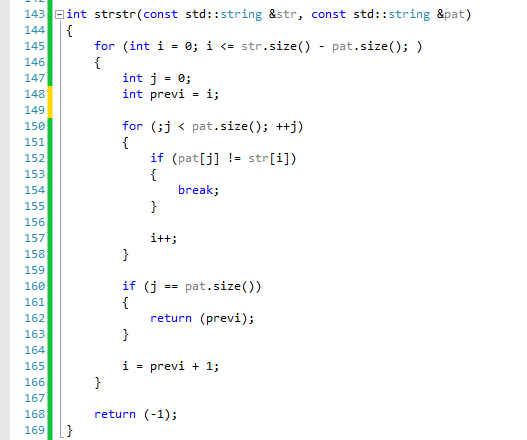
Let's start first with the original problem. We would like to implement the function: int strstr(const string &Str, const string& Pattern);
Most of us have had the chance of implementing this function at some point or another during our careers. The brute force solution of this function entails two loops, one over Str and one over pattern. Let's see it:
What is the runtime complexity of this algorithm? Since we are running in two loops and for each i we are trying all j's, we have a worst-case complexity of O(N*M) where N is the size of Str and M is the size of Pat. Can you spot where the inefficiency comes from? The problem is that if we can't find a match we have to go back (with i) and start over from where we left off when we started the match. Why are we doing this? let's look at two examples:
* str = "abcbcefg" and pat = "bce". In this case we start the match at i = 1 and j = 0, we continue to i = 2 and j = 1, but then at i = 3 and j = 2 we have a mismatch. Our algorithm will detect this mismatch and will set "i" to be 2. But what's the point? for i = 2 we already know that there will be no match. In fact, based on strwe should not be setting "i" to a previous index, but we could just as well continue advancing i.
* str = "abababc" pat = "ababc". In this case, we will start matching at i = 0 and will reach i = 4 when we detect a mismatch. We will then return to i = 1 and start again. When we reach i = 2 we will detect that the strings match. The observation is, that we should not have even bothered returning to i = 1 we could have set "i"to 2. But, if we look even closer we may notice that after we matched str = "abab" and pat = "abab" we already have one pair of "ab" in pat which we know that can be used for future matches.
The two examples are a great segway to explain how KMP works and why it is so efficient. KMP starts off by building a prefix table for pat. This prefix table will be used to indicate for each index "i" how much we have matched thus far and use this information to jump back only by the amount needed.
Lets see how the prefix table will look like for different patterns:
pat = "ababc" will result in the table: [0,0,1,2,0]
pat = "ississi" will result in the table: [0,0,0,1,2,3,4]
pat = "abcd" will result in the table: [0,0,0,0]
Notice what is happening here ? when we detect a prefix that we have seen (such as the second "ab" in "ababc") the numbers in the table indicate the size of that prefix. So if we start matching "abababc" with "ababc" for i = 4 and j = 4 we see that 'a' is different from 'c', and hence we have a mismatch. Using the table above we see that the table at index j - 1 = 3 has the value 2. We can have "j" jump back two indexes from 4 to 2, and continue our match from there. We don't have to touch "i" anymore, we just modify "j" based on the maximal size of the prefix that we have seen thus far.
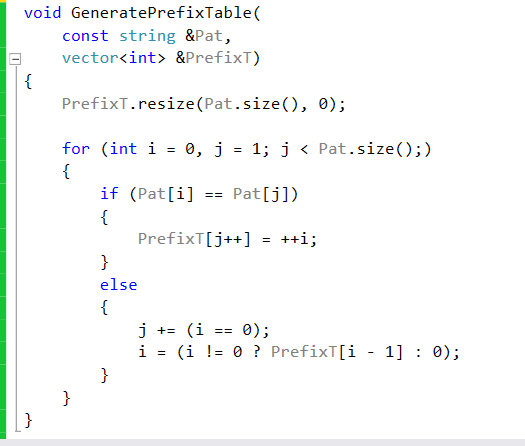
Lets see the code to generate the Prefix table:
We allocate the prefix table to be the size of "Pat". We use two indexes to fill the table. The first is "i", it will indicate the end of the current prefix. The second is "j" which will be used to find the next occurance of the prefix. Notice that "j" starts from index 1. As we are traversing we check to see whether Pat[i] == Pat[j]. If they are, then we know that there is a prefix of size i + 1 that we have encountered at index "j". We update the table at index "j" to indicate this prefix, and update "i" as well. If they are not the same, then we have two cases: First, if i == 0, it means that we have not found any prefix thus far and we just increment "j". However, if i > 0, we keep "j" where it is and make "i" go back to the index where the prefix has started and compare it again with "j" . To better explain this scenario I will show an example:
Pat = "aabaabaaaab". The prefix table for this will be: [0,1,0,1,2,3,4,5,2,2,3]. When j = 1, we have our first match and i is increment to 1. However, for j = 2 we have a mismatch Pat[i = 1] != Pat[j = 2] and "i" goes back to 0. When j = 3, things start becoming more interesting. We set PrefixT[3] = 1. For j = 4 we have a prefix of size 2 matching, "i" becomes 2 and PrefixT[4] = 2. For j = 5 we have a prefix of size 3 matching (e.g. "aab") we update "i" and "j again. In fact we continue to have more matches up to j = 8 when Pat[j = 8] = 'a' and Pat[i = 5] = 'b'. At that point since i > 0 we don't advance j but we move i to be i = PrefixT[i - 1] = 2. Pat[i = 2] = 'b' while Pat[j = 8] = 'a' which is again a mismatch. We set i = Prefix[i - 1] = 1. In this case we have Pat[i = 1] = 'a', which is equal to Pat[j = 8], and so PrefixT[8] = i + 1= 2. We increase i by 1 to i = 2 and increase j by 1 to j = 9. Since Pat[i = 2] == Pat[j == 9] we set PrefixT[9] = i + 1 = 3. What does it tell us ? It tells us that at index 9 (the end of Pat) we have been able to match a prefix of size 3 of Pat (e.g. "aab"). So even though we had a slight mismatch at index j = 8 and i = 5, we used this prefix table to jump back as much as needed based on the previous prefix match so that we can continue matching afterwards.
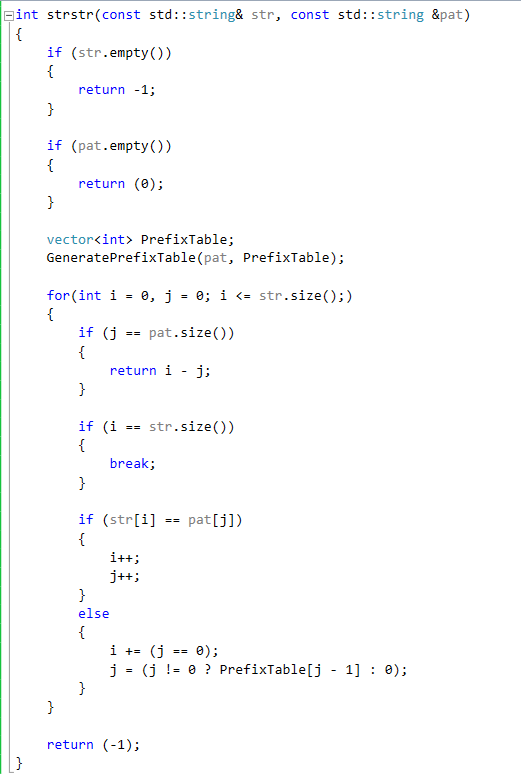
We are now ready to see the full algorithm and how it uses the prefix table.
Notice how we use the Prefix Table only when a mismatch occurs and if "j" which in this case points to pat is greater than 0. The runtime complexity of this new version in the worst case will be O(N) the size of str.
Now we have reached the second part. In this part we will show how to solve an interesting problems using KMP algorithm.
The problem asks us to convert a string to a palindrome by appending at its beginning the minimum number of letters. For example: "aacecaaa" can be turned into a palindrome by appending a single "a" at its beginning. Furthermore, consider the following string: "abcd" to turn it into a palindrome we need to append "dcb" at its beginning. What about the string "abba"? Since it is already a palindrome, we needn't append anything at its beginning. The problem asks us to return the palindrome string after we appended the letters to it.
With a brute force approach, we may try to find the longest palindrome from the beginning. Everything after that consists of letters that we need to append (in reverse order) to the beginning. Finding the longest palindrome is a task that takes O(N^2) time, unless you are familiar with Manacher's algorithm in which case you can turn it into a O(N) time algorithm. Manacher's algorithm is very complicated and so we will instead use a different approach that will leverage KMP and will take us o(N) time as well.
An important observation about palindromes is that their prefix (up to the center) is equal to the reverse of their suffix (from the center until the end). It would be nice given a string Str to know how much are the prefix and suffix (from the center) of Str alike. For example, "aacecaaa", we notice that this is almost a palindrome. The last "a" of the string is making it a non-palindrome. All we need to do is to append that "a" to the beginning of the string and it becomes a palindrome. In the case of "abcd" there is no suffix that is equal to a prefix. Hence, we need to append "dcb" to the beginning. Whenever you need to deal with prefixes KMP should be one of the things that come to mind immediately. In this case, we will use it in a sophisticated way.
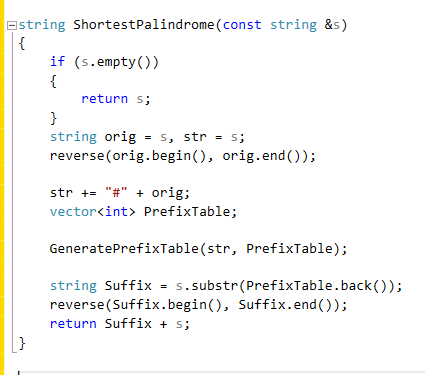
Given a string W will we generate a new string W#Wr (where Wr is the reverse of W and # is a symbol that is not in the alphabet of W). The reason we need the special character # will be clear later. By reversing W and appending it W# we can create the KMP prefix table and find out if Wr contains at its some shared characters with the prefix of W. If it does, we know that all the letters before it (e.g. from # to the value at the end of the prefix table) are letters we need to add at the beginning of W to turn it into a palindrome. Lets look again at "aacecaaa".
We will create a new string as explained above: "aacecaaa#aaacecaa" the corresponding prefix table for it is: [0,1,0,0,0,1,2,2,0,1,2,2,3,4,5,6,7]. Notice that the value at the last entry in the table is 7. This means that we have a match of size 7 with the prefix of our original string, and you can actually verify it since we have already seen that "aacecaa" is indeed of size 7. to find the letters we need to append we can either go from the # to the index of string length - 7, or we can only look at the original string and take the substring starting at index 7. In our algorithm, we will use the latter. Now we need to address the special character "#" that we added. The reason for it is not obvious. Consider the string "aaaaa". If we don't add the "#" the value at the end of the prefix table will be much larger than the size of the original string (due to the fact that the string is composed of the same character). By adding the delimiter "#" we are separating the two parts of the string (e.g. W and Wr) making sure only to seek the prefix we are interested in Wr.
We are now ready to see the code in action: