Permutation Sequence (LintCode)
Today I'll show a solution to another nice problem from LintCode: Permutation Sequence.
The description of this problem is as followed:
As the description says, the most intuitive way to solve this problem is to start enumerating all permutation until we reach the K'th one. However, this would make the problem not very interesting. We would like to solve it differently. We'll start by observing all the enumerations for N = 3 (above). We see that the numbers 1,2,3 appear as the leading digits two times each. For each instance in which 1 is the leading digit, the digits 2 and 3 appear as the second digits only once, and as the third (and last) digits only once. What if we would have had N = 4 ? In this case 1,2,3,4 would appear as the leading digits six times each (4*6 = 4!). For each instance that they appear as leading digits, we have the rest of the digits appearing 2 times each as the next one in line (just like the case of N = 3) and the leftover digits appearing as second to last 1 time each yet again ....
This observation should hint us to a potential solution. We can find the next leading digit based on K and N. If N = 3 and K = 4 it means that the permutation that we are looking for starts with 2. Why ? Because we have observed that each leading digit appears two times in the total permutations of the numbers 1 - 3. In other words since we have buckets of size 2 for each leading digit, we can find the leading digit by (K-1/Bucket Size) Notice that we need to scale K from 1 - K to 0 - (K-1) scale. So we can find the first leading digit... what about the next leading digit ? lets continue with our example of N = 3 K = 4. Once we found the bucket that the K'th number falls into, we can get rid of the leading digit as we will not need it anymore. We are left with digits 1 and 3 in this order. Since we have two digits we can be in either the permutation 2 1 3 or the permutation 2 3 1. Which one is it ? luckily we can apply the same logic using K to find which of these two we need to choose. Since our buckets are of size 2, K - 1 % 2 will tell us which of the two options we need to choose. In this case we choose the second permutation. We will apply the same logic exactly to find the last digit.
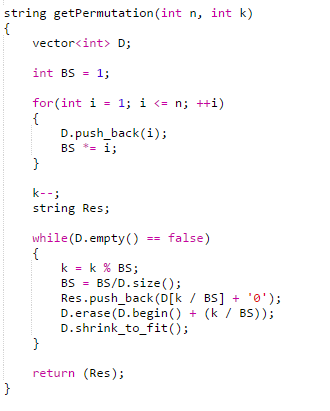
The logic is now clear. However, looking closely it seems that we still need to order the permutations in some way so that we can choose the right permutation based on K. Do we really need to order the permutations ? Actually we don't. We only need to enumerate the digits in their natural ordering - 1 2 3 4 ... N . We pick the next digit based on K and the bucket size which is of size N!/N = N-1! . Once we find our digit, we remove it from the list and leave the other digits in tact. We return to choose the next digit from the list by performing the logic described above, but this time we adjust the bucket size to be (N-1!)/N-1 = N-2! and using (K - 1)% (Old Bucket Size) as our new K. We continue this iterative process until we are left with no digits.
Now that we understand the logic, lets look at the code: