Find The smallest Number that can be created by a string of digits`

The following fun problem is defined as followed:

Given a string of digits S and a number K, return the smallest integer number that can be created by deleting K digits from S while preserving the relative locations of the digits.

As an example Lets assume S = "914123107" and K = 3, the result should be "112107". if S = "19819934101" K = 6 , the result should be: 11101.

Lets design the algorithm using our inductive approach on the size of S = N. we will denote P(1,N,k) - our final result of finding a string representing the smallest number using digits from S[1,N] by deleting K characters.

Our first non trivial base case is obviously for N equal to K + 1. It is easy to see that for N <= K the result is the empty string. So for P(i,i + K+1,K) we will only return a string with a single digit. That is the smallest digit out of the K + 1 digits of S. 

Lets assume that we can solve P(1,n < N, K) for all K.

How do we solve P(1,N,K) = ?

We first as always need to reduce the problem size in a smart and efficient way. Let the result of P(1,n < N,K) be a string S'[1...i]. The number of digits that we erased from S to get to S' is K, however some of these erased digits (especially those that follow i in S) can still be part of our solution. So we can't ignore digits i through N. However, all the digits before i in S that do not appear in S' can't be used anymore. Let the total number of these digits be K'.

So we can remove them from our general count of K and get a smaller problem P(i,N, K - K'). The problem is that our hypothesis is not strong enough to give us this ability, and hence we need to strengthen it to give us back i and K'.

P(1,n< N, K) - we know how to return a string representing the smallest number created from characters in S[1...n] after erasing K characters, and return the index i of the last character of the result in S as well as the total number of characters that come before i in S, K'.  Now that we have a stronger induction hypothesis, we can reduce the problem from P(1,N,K) to smaller sub problems. We start by looking at the char representing the smallest digit in a window of the first K + 1 chars of S. let the index of this char be i.  Based on our previous discussion we know that the first i characters are not part of the solution and so we reduce the problem to P(i + 1,N - i,K - i). According to our induction hypothesis we know how to solve this problem. Let S' be the solution of this problem, all that is left is to append S[i] to the front of S' and we have our solution.

What is the run time of this algorithm ? Finding the first character takes at most K + 1 steps. The number of iterations is at most N - K - 1. Hence, we have a total of (K + 1) * (N - K - 1) steps which give us O(K * N).

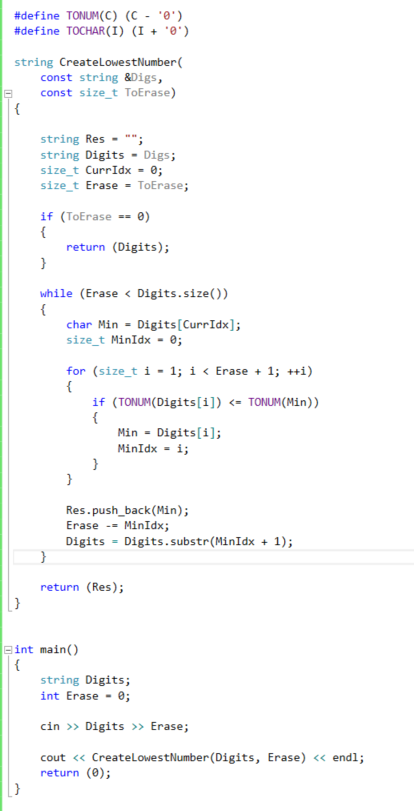
Lets now view the code:

The outer while loop terminates after our base case, that is when K is greater or equal to S. Inside that loop we find the index of the minimum digit character in a K + 1 windows. We insert that character to the result, and proceed by updating the string S (named digits) to reflect the next sub problem to be solved as well as decrease K by the number of characters that came before the index i that we found.