Think Data Science–Pitfalls
In my last post and generally I like to talk up how useful a data science approach is to understanding your data but in this post I want to sound a note of caution as it can be easy to get carried away and generally if the results look to good to be true that’s because they usually are!
Disclaimer: This post is one of a series about data science from someone who started out in BI and now wishes to get into that exciting field so if that’s you read on if not click away now
Over Fitting
If we go back to the example about delegates in my last post not turning up for community technical events then if the model we build can predict at a level of 99.99% accuracy then that’s probably because one of the features (other columns in the dataset) used to make the prediction is directly correlated to the label (the answer). In this scenario we might have a column for which size of t-shirt they were given at the event and if the column has null in it they didn’t get one. T-shirts are very popular at events so the only reason for a null in that column would be that they weren’t there and so this column matches the attendance very well but of course is useless because can’t itself be predicted before the event. This is the sort of thing that is referred to over fitting in data science
Confusion Matrix
Without the t-shirt column the accuracy of our model might drop to 94% i.e. 94 times out of a hundred we can say whether a delegate turned up or not against whether they actually did or not. That might seem a pretty good result but if we have an attendance rate of 80% i.e. 80 out of a hundred delegates turn up then if all we do is predict everyone will turn up will get us an accuracy of 80% anyway. So what is more interesting to data scientists is the confusion matrix, a set of analysis performed by comparing the models predictions against a set of data it hasn’t seen before where the out come is known and can be compared to the prediction:
I have taken this example from the Azure Machine Learning workshop Amy and I have developed and here we can see the true positives/true negatives and false positives/negatives. If this was an evaluation of event attendance and the positive label of 1 indicates that a delegate didn’t attend/ show up and a negative label of 0 means they did then we can infer the following from a test data set of 480,731 delegates across a variety of historical events:
- true positives = the model correctly predicted the non-attendees = 67,419
- true negatives = the model correctly predicted those who did actually attend = 375,695
- false positives = those the model predicted would not attend but did = 6,409
- false negatives = those the model predicted would attend but did not = 31,208
The definitions for the other numbers are as follows:
Accuracy |
the true results (both negative & Positive) / overall total | (67,419+375695)/480731 = 92.2% |
| Precision | the true positive result/ the positive results | 67,419/(67419+6,409) = 91.3% |
| Recall | true positive results/ (true positives + false negatives) | 67,419/(67,419+31,208) = 68.4% |
| F1 score | 2*(Recall * Precision)/(Recall + Precision) | 2*(0.684*0.913)/(0.684 +0.913) = 0.781 |
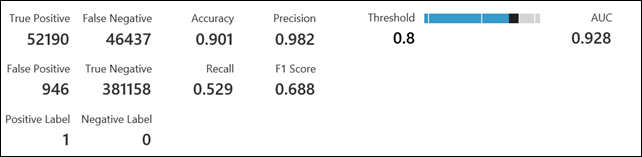
All this is based on a threshold of 0.5 meaning that the label is set to 1 when the scored probability is > 0.5 and 0 otherwise. In other word if there is more than a 50% chance of a delegate turning up then score them as predicted to turn up. In Azure ML we can move the threshold higher or lower to affect these scores e.g. only score them as predicted to turn up if the scored probability is say to 0.8 (80%) then we get this for our confusion matrix:.
so while the number sum of the true answers (positive & negative) goes up from 433,348 to 443,114 and the false positive drops as well there are now another 15,229 false negative cases (where the model thought a delegate would not turn up but they did.
So how we use this result and move the threshold is just as important as the accuracy of the numbers. For example if we want to give every delegate a t-shirt (assume for a moment they are all one size) how many should we order? A simple but effective approach would be to add up the scored probabilities for each individual to estimate the number of no shows and subtract that from the number of registrations for the event. so imagine if we have four delegates have registered each with a score 0.25 (25%) of NOT attending from this model adding this up gives 1 which we subtract from the 4 registration and only order 3 shirts because across all four of them it is extremely likely (but not certain) that only three will attend. I say not certain because the prediction might not be very good for small events but as the registrations for an event get larger then the accuracy improves. So if I download the scores from the model I have been using and sum the scored probabilities across the 480,731 examples in the sample I get 98,816 as my predicted no shows which compares very well with the 98,617 actual no shows.
A good way of think about this is that statistics is analysis of the behaviour of large groups of thinks (called the total population) based on the behaviour of a sample of that population. We don’t know for sure that this is the case but we can work out the probabilities involved to make a bridge between what the sample behaviour is and apply that to the whole.
Finally if you want to follow along you’ll need nothing more than a modern browser and spreadsheet tool that can work with .csv files and can handle 400,000 rows of data and I’ll write this up in the next post.
Note: I can’t share the actual data for the events model as the data and model aren’t mine.